Muchas veces habrás oído hablar de los intervalos musicales, de la quinta justa, la tercera Mayor, la trecena o la cuarta descendente y posiblemente te habrá sonado a chino.
Quizás ya sabes de lo estamos hablando, pero tienes dudas sobre otros temas, como su clasificación, la inversión de los intervalos, etcétera.
O puede que ya conozcas la Teoría de los Intervalos y la manejes con fluidez.
En este artículo te ofrecemos la explicación completa. También veremos algunos trucos para memorizarlos mejor.
El conocimiento y manejo fluido de los intervalos es imprescindible para el posterior estudio de las escalas, acordes, modos, grados, tonalidades, etc.
¿Qué es un intervalo musical?
Un intervalo musical es la distancia entre dos notas, respecto del tono o altura de cada una de ellas.
El intervalo se mide en notas naturales o grados, tonos y semitonos.
Hay varios tipos de intervalos: tonales y modales, ascendentes y descendentes, simples y compuestos, complementarios, ascendentes y descendentes, consonantes y disonantes.
Los intervalos también se pueden clasificar como armónicos o melódicos, dependiendo de si las notas suenan simultáneamente (armónicos), o por separado (melódicos).
El primer paso para descubrir dónde están las notas en el diapasón de la guitarra o de la formación de escalas y acordes es el conocimiento y manejo de los intervalos.
Antes de pasar a ver los tipos de intervalos y su clasificación, hemos de conocer de qué están compuestos, y es de tonos y semitonos.
Tonos y semitonos
Un tono es la distancia entre dos notas sucesivas, con diferente nombre. La distancia de un tono está entre todas las notas naturales (sin alteraciones) correlativas. Hay dos excepciones: entre E y F y entre B y C, entre las cuales hay un semitono.
También se da el caso de distancia de semitono entre dos notas del mismo nombre. Lo veremos con más detalle más adelante.
Semitono, definición y tipos
El semitono es la distancia más corta entre dos notas sucesivas en el sistema temperado (división de la escala en 12 partes iguales, TET), usado en la música occidental.
Una octava está compuesta de doce partes iguales.
La octava es el intervalo que hay desde una nota hasta la siguiente de igual nombre, pero de sonido más agudo.
Un semitono es la doceava parte de la octava.
En la guitarra, la distancia de semitono es de un traste.
Semitonos cromáticos y diatónicos
Los semitonos pueden ser cromáticos o diatónicos.
El semitono cromático es la distancia entre dos notas con el mismo nombre, pero diferente entonación.
El semitono diatónico es la distancia entre dos notas de diferente nombre.
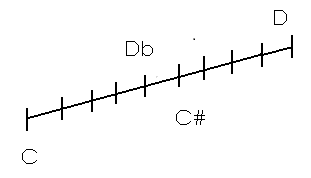
Este gráfico explica cómo desde la nota Do (C) hasta Re (D) hay una distancia ascendente. Desde C hasta D hay un tono entero. Se ha dividido en nueve partes, que simulan las 9 comas o cambios de colorido en el sonido que el oído humano es capaz de distinguir.
La división no es simétrica ya que, si sumamos al primer sonido (C) cinco cromas, tenemos la distancia de un semitono cromático (desde C hasta C# [desde do hasta Do sostenido]). Y si restamos cinco cromas al segundo sonido (D) tenemos otro sonido cromático (de D a Db [de RE a Re bemol]).
Por tanto, el semitono cromático se produce entre dos notas con el mismo nombre:
Entre C y C# hay un intervalo cromático porque las dos notas comparten el nombre (C) aunque su sonido es diferente. Una nota es natural (C) y la otra tiene un sostenido (C#). Esta última es un semitono cromático más alta que la primera.
El semitono entre D y Db es el mismo caso que el anterior, pero, en este caso, lo que hay es un semitono cromático descendente.
Por enarmonía (mismo sonido con diferente nombre, algo que ocurre en instrumentos atemperados, como lo es la guitarra), las notas C# y Db suenan igual. Estos intervalos se llaman enarmónicos.


Entre las notas C y Db hay un semitono diatónico, pues tienen diferente nombre. Igual situación concurre en el intervalo entre D-C#.
Por consiguiente, un semitono diatónico se da entre notas de diferente nombre (C-Db, si es ascendente o D-C#, si es descendente)
En los instrumentos temperados un tono es la suma de dos semitonos: dos trastes en la guitarra o dos teclas en el piano.
Qué es un tono
Un tono consta de dos semitonos. En la guitarra, un tono son dos trastes.
De estos dos semitonos, uno es cromático y el otro diatónico.
Un tono equivale a la sexta parte de la octava. Es la suma de un semitono diatónico y otro cromático. En el gráfico, la distancia de tono es desde C hasta D.
Una escala musical está construida por estructuras formadas por tonos y semitonos.
Por ejemplo, la estructura de la escala Mayor es la siguiente:
T – T – S – T – T – T – S
donde T representa un tono entero y S, un semitono.
La secuencia se culmina con la repetición de la Fundamental en octava. Puedes saber más sobre las escalas Mayores en el post sobre la Tonalidad y Escala Mayor.
¿Cuáles son las 12 notas musicales?
Las notas musicales son:
Do (C), Re (D), Mi (E), Fa (F), Sol (G), la (A) y Si (B).
Entre cada una de las notas y la nota posterior hay otra intermedia a distancia de un semitono (# o b). Este caso ocurre entre todos los casos excepto entre E y F y entre B y C.
Usaremos el cifrado americano, más práctico para la explicación:
C 1 tono D 1 tono E 1/2 tono F 1 tono G 1 tono A 1 tono B 1/2 tono C
En este gráfico, las 7 notas naturales están en verde y, entre ellas, en azul, está la distancia que las separa.
Así que hay cinco distancias de 1 tono y dos distancias de 1/2 tono.
Recuerda esto: entre cada una de las notas hasta la nota posterior hay una distancia de 1 tono, excepto entre la nota E y F y también entre B y C. Resulta más fácil memorizar las dos excepciones que las otras 5.
En los cinco casos de pares de notas que están separadas por un tono entero, hay otra nota que está a distancia de un semitono cromático.
Este semitono se consigue añadiendo a la primera nota un sostenido (#). O descendiendo la segunda nota en un bemol (b).
Como hemos explicado anteriormente, entre E y F y desde B hasta C no hay semitono intermedio.
Esta es la sucesión de las 12 notas musicales (escala cromática):
C – C# – D – D# – E – F – F# – G – G# – A – A# – B – C
o también:
C – Db – D – Eb – E – F – Gb – G – Ab – A – Bb – B – C
Recuerda que hay un semitono diatónico entre notas separadas por un tono cuando estas llevan diferente nombre. Ejemplo, desde C – Db. Y hay un semitono cromático entre dos notas consecutivas el mismo nombre C – C#.
Explicación breve sobre los casos de Mi sostenido/Fa bemol y Si sostenido/Do bemol
En la práctica de la guitarra, E sostenido es enarmónica con F bemol y B sostenido, suena igual que C. No obstante, estas notas pueden aparecer escritas en una partitura, lo que se hace para respetar tanto la teoría musical como la escritura correcta.
Por ejemplo, veamos un tema o canción en la Tonalidad de E Mayor. Esta Tonalidad tiene cuatro sostenidos, que son F#, C#, G#, D#. Entonces, aparece en la partitura la nota C natural y, a continuación, un C sostenido.
En este caso la nota C natural se representaría como B sostenido, ya que C tiene un sostenido en la armadura de la Tonalidad de E Mayor.
Veamos el ejemplo anterior más detenidamente. Imaginemos que hay un C natural y, a continuación, aparece un C sostenido. Habría que dotar al C de un signo becuadro, anularlo y volver a poner un sostenido. Es más fácil y lógico escribir B# y después C#.
En el caso de una Tonalidad con bemoles en la armadura, por ejemplo, E bemol, que tiene tres bemoles, Bb, Eb, y Ab, si aparece la nota E natural, es mejor escribirla como F bemol, ya que, en esta Tonalidad, E tiene ya bemol en la armadura.
Finalmente, estas notas existen en la teoría, pero en la guitarra, en la práctica, no se usan, ya que tienen el mismo sonido.
Tipos de intervalos y su clasificación
La clasificación de los intervalos musicales puede ser según su amplitud y especie. La amplitud del intervalo indica su extensión, cuanto mide. Y la especie según sus características, los divide en modales o tonales.
Clasificación de los intervalos según su amplitud
La clasificación de los intervalos musicales según su amplitud es: Unísono, segunda, tercera, cuarta, quinta, sexta, séptima y octava.
Según su amplitud, el intervalo indica la distancia entre dos notas contando ambas inclusive.
Por ejemplo, desde la nota C (Do) hasta la nota D (Re), el intervalo es de segunda; desde C hasta E, un intervalo de tercera; y desde C a B, una séptima. Esta es una clasificación cuantitativa.
Tipos de intervalos musicales según su especie
Los tipos de intervalos musicales según su especie son: Mayor, menor, justo, aumentado y disminuido.
Según su especie es una clasificación cualitativa e indica la calidad del intervalo. Existen dos subtipos de intervalos según su especie: modales y tonales.
Los intervalos modales pueden ser mayores o menores.
Los intervalos tonales pueden ser justos, aumentados o disminuidos.
Otras clasificaciones de los intervalos
Además de su clasificación según su amplitud o su especie, los intervalos musicales también se pueden catalogar por otros parámetros.
Intervalos armónicos y melódicos
Los intervalos armónicos son aquellos que están en disposición vertical en la partitura, o sea, que suenan a la vez, por ejemplo, las notas de los acordes están separadas por intervalos armónicos.
Intervalos melódicos están dispuestos horizontalmente. Las notas suenan en secuencia o seguidas una de otra, por ejemplo, en las escalas las notas están separadas por intervalos melódicos.
Intervalos ascendentes y descendentes
El intervalo ascendente ocurre cuando la segunda nota es más aguda o alta que la primera. Po ejemplo: desde C hasta D hay un intervalo de segunda Mayor ascendente.
El intervalo descendente, por el contrario, consiste en que la segunda nota es más baja o grave que la primera. Por ejemplo, entre D3 y C#2 hay un intervalo de segunda menor descendente.
Intervalos consonantes y disonantes
Los intervalos armónicos pueden tener un sonido que produce una sensación al oído de reposo y claridad (intervalos consonantes) o, por el contrario, más inestabilidad o tensión (intervalos disonantes).
Los intervalos consonantes pueden tener una consonancia perfecta o imperfecta.
La consonancia perfecta se da en intervalos de 8ª, 4ª justa y 5ª justa.
Los intervalos de consonancia imperfecta, lo que no quiere decir que suenen mal, sino un poco menos definidos, son la 3ª Mayor y menor y la 6ª Mayor y menor.
De igual manera, entre los intervalos disonantes se da el caso de la disonancia perfecta en la 2ª Mayor y menor y en la 7ª Mayor y menor.
Y, por último, el caso de los intervalos semiconsonantes, que es el de la 4ª aumentada y la 5ª disminuida.
Notación de los intervalos
Ahora aprenderemos cómo se cifran todos los intervalos.
Respecto al nombre de las notas, y según he aclarado más arriba, usaremos la notación anglosajona (C – D – E – F – G – A – B).
En la siguiente tabla se muestra la forma de nombrar a cada especie de intervalo con la abreviatura:
| Mayor | M |
| menor | m |
| Justo | j |
| Aumentado | aum, +, # |
| disminuido | dim, b, º |
Mayor siempre va en mayúscula y menor en minúscula.
Si no se precisa, el modo es Mayor y, si el intervalo es menor, siempre hay que especificarlo. La excepción es el intervalo de séptima, el cual es menor si no se detalla el modo.
Ejemplos:
Segunda Mayor – 2ª (no se especifica que es Mayor)
Tercera menor – 3ªm (sí se especifica)
Quinta disminuida – 5ª dim, 5b, 5º
Séptima menor – 7 (en el intervalo de séptima no se especifica nada cuando la 7ª es menor, al revés de lo que ocurre en los demás casos, y sí se precisa cuando es Mayor).
Esta regla funciona igual para los acordes. Un acorde es Mayor si no se especifica nada, excepto en los acordes de séptima, que, si la 7ª es Mayor, hay que precisarlo. Por ejemplo, Cmaj7 significa que el acorde es C Mayor y la Sétima también es Mayor. C7 quiere decir que el acorde es Mayor y la séptima es menor.
Si el acorde es menor, hay que especificar el modo del acorde, y también hay que detallar el modo de la séptima. Por ejemplo: Cm7maj significa que el acorde es C menor, pero tiene la séptima Mayor. Cm7 es un acorde de C menor con séptima menor.
Tabla de los intervalos simples
Los intervalos simples son los que están dentro de la primera octava, que no la sobrepasan.
Los intervalos compuestos son aquellas distancias entre notas mayores que la octava. Están formados por una octava completa más un intervalo simple, que puede ser una segunda, cuarta o sexta. Los veremos más adelante, en este mismo artículo.
En la siguiente tabla puedes ver todos los intervalos simples, la distancia entre sus notas y un ejemplo de cada uno.
| Intervalo | Distancia | Ejemplo |
|---|---|---|
| Unísono | Igual sonido | C -C |
| Segunda menor | 1 semitono | C-Db |
| Segunda Mayor | 1 tono | C – D |
| Segunda aumentada | 1 tono y 1/2 | C – D# |
| Tercera menor | 1 tono y 1/2 | C – Eb |
| Tercera Mayor | 2 tonos | C – E |
| Cuarta disminuida | 2 tonos | C – Fb |
| Cuarta justa | 2 tonos y 1/2 | C – F |
| Cuarta aumentada | 2 tonos y 2 semitonos | C – F# |
| Quinta disminuida | 2 tonos y 2 semitonos | C – Gb |
| Quinta justa | 3 tonos y 1/2 | C – G |
| Quinta aumentada | 3 tonos y 2 semitonos | C – G# |
| Sexta menor | 3 tonos y 2 semitonos | C – Ab |
| Sexta Mayor | 4 tonos y 1/2 | C – A |
| Sexta aumentada | 4 tonos y 2 semitonos | C – A# |
| Séptima disminuida | 4 tonos y 1/2 | C – Bbb |
| Séptima menor | 4 tonos y 2 semitonos | C – Bb |
| Séptima Mayor | 5 tonos y 1/2 | C – B |
| Octava | 5 tonos y dos semitonos | C – C |
| Intervalo | Distancia | Ejemplo |
Hay tres intervalos justos, que son la cuarta, la quinta y la octava. Estos son los intervalos tonales, básicos en la formación de la Tonalidad.
Hay 4 intervalos que pueden ser Mayores o menores. Son: intervalo de segunda, de tercera, de sexta y de séptima. Estos intervalos se denominan intervalos modales, pues son los que definen el Modo, Mayor o menor, de la Tonalidad.
Algunos intervalos son enarmónicos, lo que significa que suenan igual en instrumentos temperados. Los intervalos aumentados y disminuidos son enarmónicos entre sí. Esto implica que tienen el mismo sonido, aunque su nombre es diferente.
Por ejemplo, la cuarta aumentada y la quinta disminuida tienen el mismo tamaño, que es de tres tonos o dos tonos y dos semitonos, y también el mismo sonido. A este intervalo se le conoce también con el nombre de tritono (B-F).
Inversión de los intervalos
La inversión de los intervalos consiste en que cada uno de ellos tiene otro intervalo complementario. Sumando los dos, el resultado es la octava.
Intervalos complementarios
Intervalos complementarios son aquellos que, sumados entre sí, completan una octava. Por ejemplo, una tercera y una sexta, si las sumamos, el resultado es un intervalo de octava. Otro ejemplo: una quinta y una cuarta también ofrecen el mismo resultado en la suma.
El resultado de la suma de los tonos y semitonos de los dos intervalos inversos siempre es seis tonos o doce semitonos. Una octava está formada por seis tonos o doce semitonos
Ahora vamos a ver una forma de saber rápidamente cuál es la inversión de cada intervalo y para qué nos puede servir.
En la tabla de abajo se muestran los intervalos simples y sus complementarios. Como se puede ver, la suma es nueve en todos los casos.
| Intervalo | Complementario | Suma |
|---|---|---|
| 1ª (unísono) | 8ª (octava) | 9 |
| 2ª | 7ª | 9 |
| 3ª | 6ª | 9 |
| 4ª | 5ª | 9 |
| 5ª | 4ª | 9 |
| 6ª | 3ª | 9 |
| 7ª | 2ª | 9 |
| 8ª (octava) | 1ª (unísono) | 9 |
El resultado de todas las sumas es nueve. Este es un truco para descubrir rápidamente cuál es el intervalo complementario de cualquier otro. La suma de los dos siempre es nueve.
Por ejemplo, si quieres saber el intervalo complementario de una 5ª, bastaría con restar 5 a 9. El resultado de esta resta es 4. Por tanto, el intervalo complementario de una 5ª es una 4ª.
Como verás, es fácil descubrir qué intervalo es complementario respecto de otro, sin tener que contar tonos y semitonos.
Especies complementarias
En el siguiente gráfico están representadas las especies complementarias que corresponden a cada intervalo.
| Especie | Especie Complementaria |
|---|---|
| Mayor (M) | menor (m) |
| menor (m) | Mayor (M) |
| aum | dim |
| dim | aum |
| justo (j) | justo (j) |
Así pues, el intervalo complementario de la 2ª M es la 7ª m. En el intervalo de 5 dim, el complementario es el de 4 aum, etc.
Uso práctico de la inversión de los intervalos
La inversión de los intervalos se usa, por ejemplo, en la guitarra, para identificar un intervalo demasiado grande a partir de otro más pequeño o para encontrar intervalos a partir de su complementario.
Un caso práctico del uso de la inversión de los intervalos es: si quieres encontrar la 7 Mayor de la nota E de la sexta cuerda al aire, puedes ir a su octava, en el traste XII y ahí está, un traste más atrás, o sea una segunda menor descendente que es la inversión de la séptima Mayor.
Intervalos Simples y Compuestos
Los intervalos simples son todos los que hemos visto hasta ahora: Unísono, Segunda, Tercera, Cuarta, Quinta, Sexta, Séptima y Octava.
Los intervalos compuestos son los que se producen más allá de la octava. Son compuestos porque están formados por una octava completa más un intervalo simple.
Son intervalos compuestos:
| Intervalo Compuesto | Intervalo Simple + Octava |
|---|---|
| 9ª (novena) | 2ª |
| 11ª (oncena) | 4ª |
| 13ª (trecena) | 6ª |
Pudiera parecer que hay más intervalos compuestos. Matemáticamente, sí los hay, no obstante, los intervalos compuestos mayores que el de trecena, no se usan. El motivo es que no sirven para la construcción de acordes o escalas ni para los demás usos que pueden darse en la aplicación de la Teoría de los Intervalos.
La inversión de los intervalos compuestos funciona del mismo modo que la de los simples. Tan sólo se invierte el intervalo simple, al que se le suma la octava.
Los intervalos en la Guitarra
Es muy importante visualizar los intervalos en el diapasón de la guitarra. Se pueden memorizar fácilmente aprendiéndose algunos dibujos que forman con respecto a la primera nota.
Ejemplos:
- El intervalo de cuarta justa está en el mismo traste que la nota original, en la cuerda inferior.
- La quinta justa, dos trastes más adelante y una cuerda más abajo.
- La octava, dos trastes más adelante y dos cuerdas más abajo.
Con este método podemos aprender los intervalos en el mástil. Ahora usaremos la inversión de los intervalos para aprender los complementarios.
Ejemplo: un intervalo de segunda Mayor está situado dos trastes más adelante, en la misma cuerda. Por consiguiente, el intervalo complementario de esta segunda Mayor, que es la séptima menor, estará situado dos trastes hacia atrás, también en la misma cuerda.
Teniendo en cuenta el dibujo en el diapasón que forma un intervalo de sexta menor, por ejemplo, podremos deducir que su inversión es la tercera Mayor. Y de esta manera podemos proceder con todos los intervalos y sus inversiones.
Hay que considerar que la relación entre todas las cuerdas es de una cuarta respecto de la cuerda de arriba, excepto entre la tercera y la segunda, que es una tercera Mayor (G-B). En este caso, el dibujo de los intervalos cambia un traste menos.
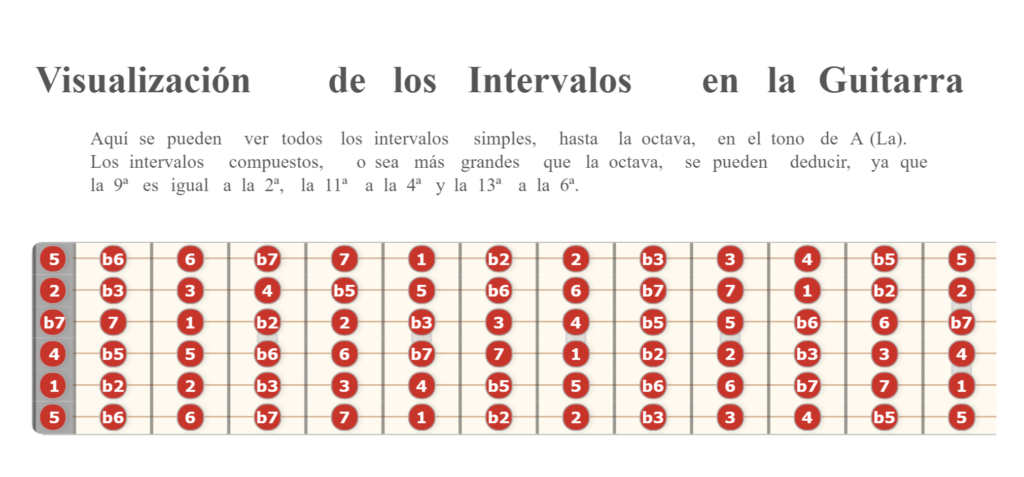
En el siguiente gráfico puedes visualizar los intervalos simples partiendo desde la nota A (La).
Los intervalos compuestos se pueden deducir a partir de los simples, ya que la 9ª es igual a la 2ª, la 11ª, igual a la 4ª y la 13ª, a la 6ª.
Preguntas frecuentes. FAQ
Un intervalo musical es la distancia que hay entre dos notas. Se mide en tonos y semitonos.
Los intervalos musicales se pueden clasificar según su amplitud o según su especie.
Según su amplitud, un intervalo musical puede ser de unísono, de segunda, tercera, cuarta, quinta, sexta, séptima, octava, novena, oncena y trecena.
Según su especie, los intervalos musicales se clasifican en Mayores, menores, justos, aumentados y disminuidos.
Cada intervalo tiene otro complementario, la suma de los cuales da como resultado la octava. Es decir, entre un intervalo y su inversión deben sumar doce semitonos o seis tonos enteros.
Los intervalos simples son lo que van desde el unísono hasta la octava y los compuestos son los que sobrepasan la octava y son la suma de ésta más otro intervalo simple.

